A Quick Summary

Introduction

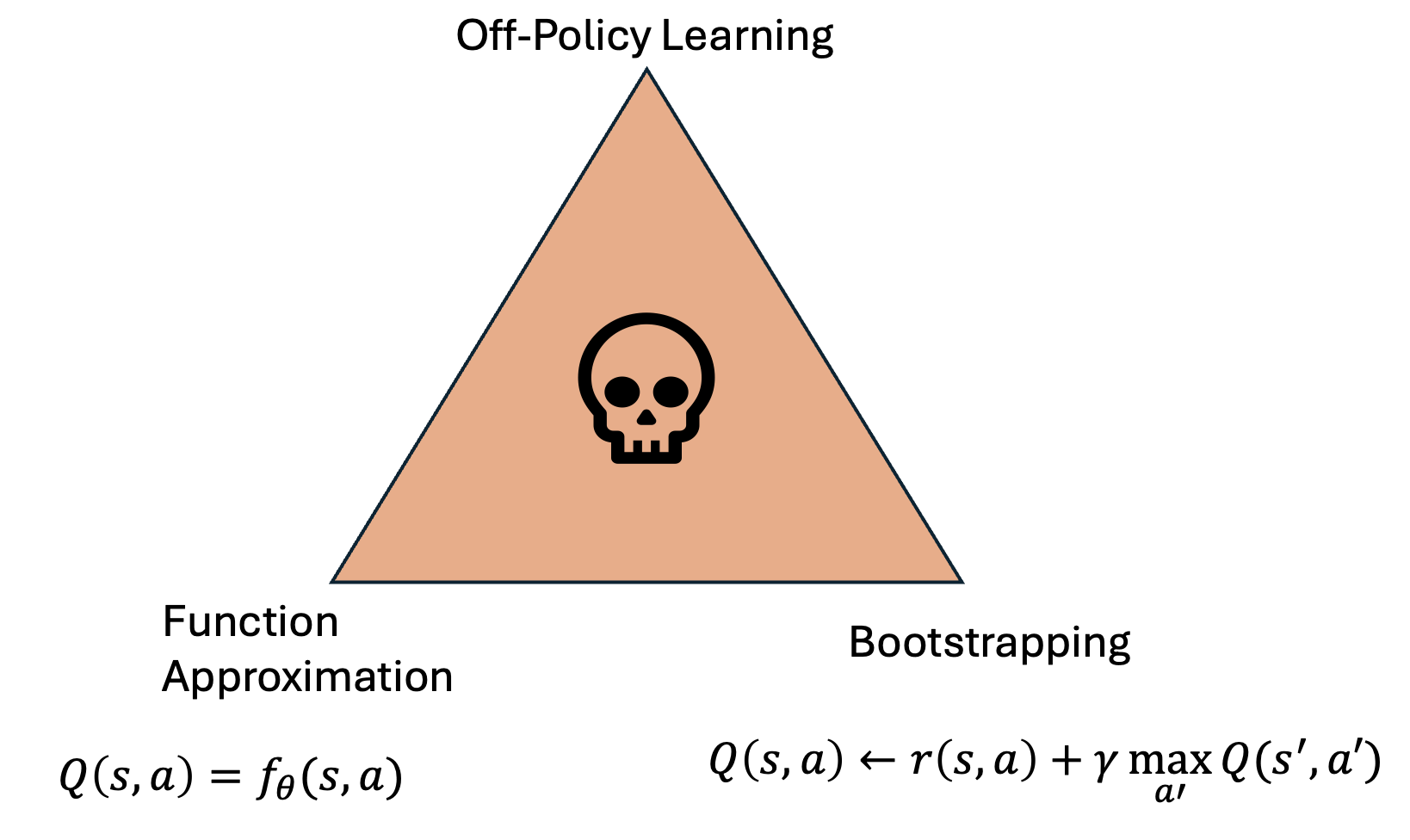
Reinforcement Learning is tasked with the goal of finding a policy that maximizes cumulative reward. Off-policy algorithms form an important part of RL algorithms as they are by definition able to leverage data from arbitrary policies in order to optimize the current policy. In practice, most off-policy deep RL algorithms suffer from issues like training instablity and overestimation.

Experiment: SAC fails when a little expert data is added to replay buffer

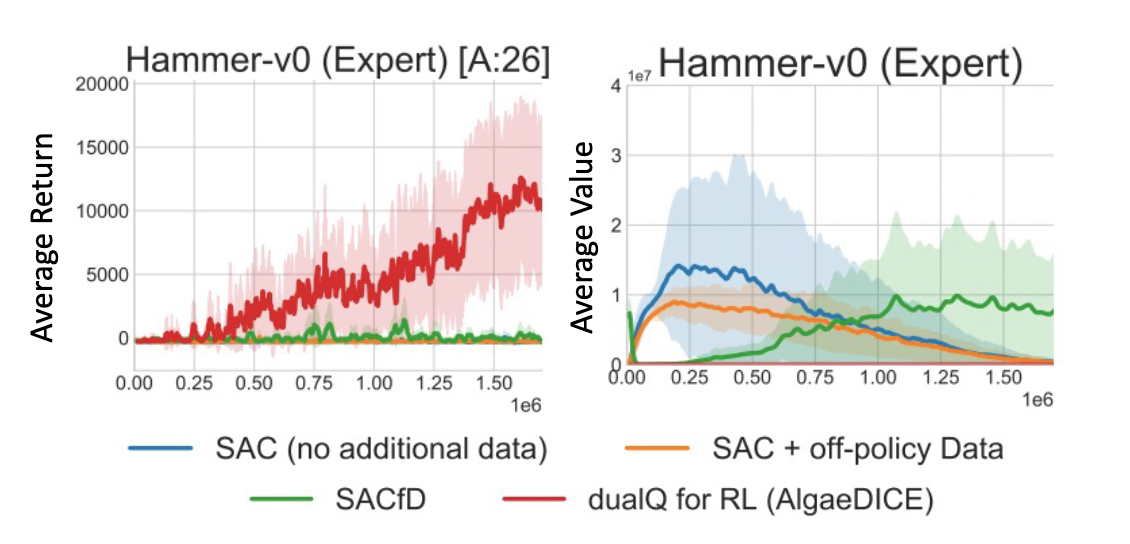
We do a simple experiment to verify a phenomena already known in literature. We take SAC, a stable, well-known and a goto methods for off-policy deep RL and before the start of training we add a few expert trajectories to the replay buffer. A good off-policy agent should be able to leverage the information provided by expert trajectories to direct exploration and learn faster. Instead, we see that SAC learning crashes (even with specialized fixes). This is likely due to the deadly-triad of learning off-policy with function approximation and bootstrapping. Sneak Peek: Dual-RL algorithms are able to leverage the expert data to actually learn faster.

A number of performant off-policy methods have emerged recently (CQL, ATAC, XQL, IQ-Learn, etc) that attribute their success to various different aspects of the algorithm and have widely differing mathematical derivations. We ask ourselves in this work: Is their a common thread that unifies a these performant algorithms?

Our work not only answer the question in affirmative, but also provides a way to unify reinforcement learning and imitation learning algorithms as well as offers new insights into algorithms to make them even better!

Things to know

In this work, we rely of $f$-divergences which are informally a measure of distance between two distributions and given by:

\(D_f(P\|Q) = \mathbb{E}_{z\sim Q}[f(\frac{P(z)}{Q(z)})]\) where P, Q are two distribtuions and $f$ is a convex function. Another important concept is the convex conjugate definition. A convex conjugate $f^*$ of function $f$ is given by:

\[f^*(y)= \text{sup}_{x\in \mathbb{R}} [<x \cdot y> - f(x)]\]

We extend the definition and present a convex conjugate with positivity constraint:

\[f^*_p(y)= \text{sup}_{x\in \mathbb{R}} [<x \cdot y> - f(x)]~~~s.t.~~x>0\]

For readability, we also use the two backup operators below later in the blog:

\[\text{Q-backup Operator} ~~~ T^\pi_r Q(s,a) = r(s,a)+\gamma \mathbb{Q}_{s'\sim p(\cdot|s,a),a\sim \pi(s')}[Q(s',a')]\]

and

\[\text{V-backup Operator} ~~~ T_r V(s,a) = r(s,a)+\gamma \mathbb{V}_{s'\sim p(\cdot|s,a)}[V(s')]\]

Essentially, Q is the backup of reward plus expected next-Q and V is the backup of reward plus expected next V.

The Primal RL problem

Visitation distributions provide an easy way to think about the RL objective. A visitation distribution is a distribution over state-action space specifying the average (discounted) probability that a policy will reach that state and take the action when starting from the initial state distribution. Visitation distributions are denoted by $d(s,a)$.

A general objective for regularized reinforcement learning can be written in terms of maximizing expected reward under the visitation distribution while being regularized to some offline vistation distribution denoted by $d^O(s,a)$.

\[\max_\pi \, J(\pi)=\mathbb{E}_{d^\pi(s,a)}[r(s,a)] -\alpha D_f(d^\pi(s,a)\|\|d^O(s,a))\]

Searching over the space of visitation distributions is hard, because not all visitation distributions are possible in the environment. A policy when acting in the world has to respect the worlds dynamics! Well, let’s make the problem a little more formal by specifying the exact optimization problem we wish to solve:

\[\texttt{primal-Q} ~~~~~~~~~~\max_\pi J(\pi) = \max_\pi \big[\max_{d} \; \mathbb{E}_{d(s,a)}[r(s,a)]-{\alpha}D_f(d^\pi(s,a)\|\|d^O(s,a))\] \[\text{s.t}~~~~~~~~~ d(s,a)=(1-\gamma)d_0(s).\pi(a|s)+\gamma \textstyle \sum_{s',a'} d(s',a')p(s|s',a')\pi(a|s), \; \forall s \in \mathcal{S}, a \in \mathcal{A} \big]\]

All we have done above is added a constraint, popularly known as the bellman flow constraints which specify the condition which a visitation distribution should follow to be valid under the environment dynamics and initial state distribution. It is actually possible to make the constraint only depend on state-visitation distributions without changing the optimal solution:

\[\texttt{primal-V} ~~~~~~~~~~\max_{d \geq 0} \; \mathbb{E}_{d(s,a)}[r(s,a)]-\alpha D_f(d^\pi(s,a)\|\|d^O(s,a))\\\] \[\text{s.t} \; \textstyle \sum_{a\in\mathcal{A}} d(s,a)=(1-\gamma)d_0(s)+\gamma \sum_{(s',a') \in \mathcal{S} \times \mathcal{A} } d(s',a') p(s|s',a'), \; \forall s \in \mathcal{S}.\]

Solving the RL problem in the primal land is hard as the constraints have to be accounted for. Convex optimization provides us with tools to create a dual problem for these objectives which share the same optimal solutions and are unconstrained.

Dual RL: Objectives

Our primal problems are convex with linear constraints. This means we can attempt computing a Lagrangian dual and analyzing if they help us solving the optimization more easily. Taking the Lagrangian dual and using the convex conjugate definition we get the following two duals corresponding to primal-Q and primal-V.

\[\texttt{dual-Q}~~~~~~~~~~\max_{\pi} \min_{Q} (1-\gamma)\mathbb{E}_{s\sim d_0,a \sim \pi(s)}[{Q(s,a)}] +{\alpha}\mathbb{E}_{(s,a)\sim d^O}[{f^*\left(\left[ T^\pi_r Q(s,a)-Q(s,a)\right]/ \alpha \right)}]\]

and the other dual:

\[\texttt{dual-V}~~~~~~~~~~\min_{V} {(1-\gamma)}\mathbb{E}_{s \sim d_0}[V(s)] +{\alpha}\mathbb{E}_{(s,a)\sim d^O}[f^*_p\left(\left[\mathcal{T}V(s,a)-V(s))\right]/ \alpha\right)],\]

Indeed the duals look easier to optimize. They are unconstrained, naturally off-policy as they require only sampling from $d^O$ and have the unique property that the gradient with respect to $\pi$ is the on-policy policy gradient computed using off-policy data. Moreover, dual-V is a single variable optimization making learning much easier compared to the traditional 2-player actor critic learning setup.

Bridging Offline RL with Dual RL

Dual RL helps us get a clear understanding of offline RL algorithmic landscape. These approaches have been developed using widely differing derivations and we show in the paper that they are essentially the same approach under the lens of dual RL. Our hope is that this unification allows the researchers to analyze a number of RL algorithms with a common foundation and for practioners to carry over design choices across methods that are instantiated under the same setup.

The common idea in offline RL is to penalize the policy to go away from the offline dataset distribution. This is enforced by a policy constraint or a state-action visitation constraint. More recently, a number of approaches have emerged that use the idea of pessimistic value function (CQL, ATAC, etc) or implicit maximization (IQL, XQL, etc) to develop more performant offline RL methods. Pessimistic value function aims to achieve a lower bound on value functions and implicit maximization only uses observed samples to compute the maximum. It remains unclear how the two new classes of methods relate to the popular policy/visitation constraint in offline RL.

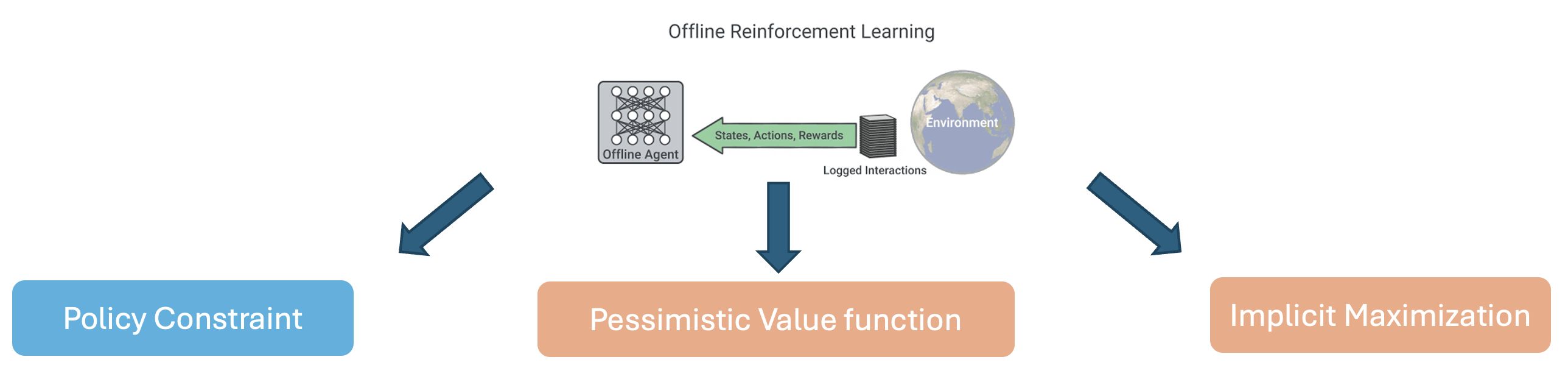
Dual RL helps us connects the dots by showing that the pessimistic value methods are dual-Q variant of the policy/visitation matching primal and implicit maximization methods are dual-V variant of policy/visitation matching methods.

Dual-V Learning ($f$-DVL): A new class of offline RL methods

The $\texttt{dual-V}$ objective gives a new class of methods parameterized by the choice of function $f$ for offline RL.

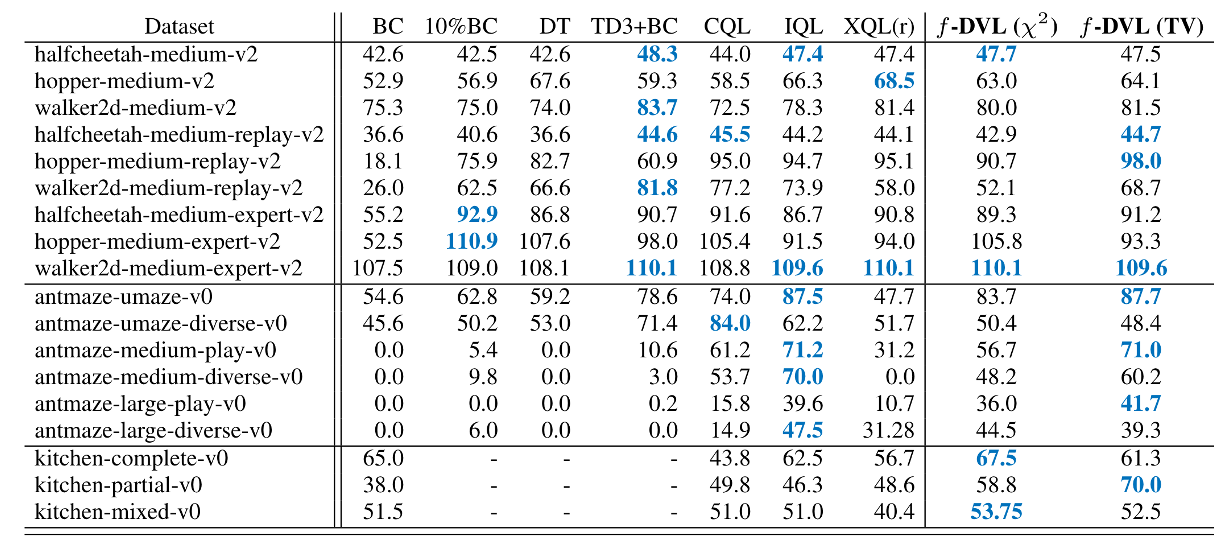
\[\texttt{dual-V}~~~~~~~~~~\min_{V} {(1-\gamma)}\mathbb{E}_{s \sim d_0}[V(s)] +{\alpha}\mathbb{E}_{(s,a)\sim d^O}[f^*_p\left(\left[\mathcal{T}V(s,a)-V(s))\right]/ \alpha\right)],\]

Extreme Q-learning (XQL), a implicit maximization based offline RL method, was derived using the hypothesis that Bellman errors are Gumbel distributed. In face, XQL can simply be seen as a special case of $f$-DVL when $f$ is chosen to be the reverse-KL divergence. The choice of setting $f$ corresponding to reverse KL divergence leads to a exponential conjugate which makes learning unstable due to exploding gradients. Choosing divergences with low-order $f^*_p$ can lead to stable off-policy algorithms. Our experiments rely on Total-Variation and Chi-square divergences to obtain across the board improvements.

Bridging Offline IL with Dual RL

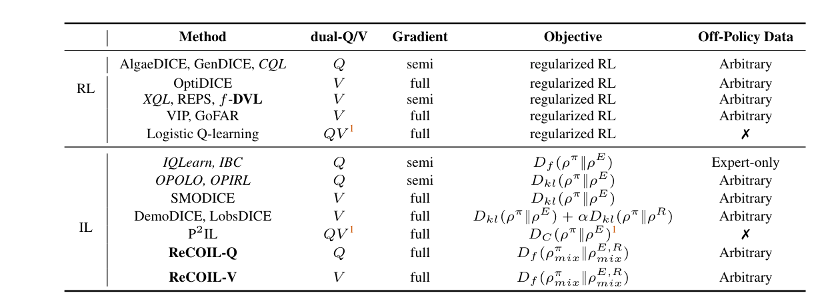
Interestingly, from the perspective of Dual RL, there is not really any difference between imitation learning and reinforcement learning. Simply setting the reward function to zero gives us the imitation learning objective and all the previous derived methods follow again with reward function=0. We can see that some recent algorithms shown in the right table (notably implicit behavior cloning and IQLearn) are just dual methods in disguise.

A limitation of existing imitation methods is their inability to handle off-policy data. We should be able to handle the more practical situation where we have a large amount of possibly suboptimal data $d^S$ + a few trajectories demonstrated by expert $d^E$. The offline dataset is a source of information about dynamics of the environment and should be used to do better imitation learning. Prior methods have created lower bounds to THE imitation objective to leverage offline data.

ReCOIL: Imitation learning with arbitrary suboptimal data + expert data

We propose to use the following mixture distribution matching objective.

\[D_f(\beta d(s,a) + (1-\beta) d^S(s,a) \| \beta d^E(s,a) + (1-\beta) d^S(s,a))\]

It is a valid imitation learning objective as it is only minimized when the visitation of agent matches that of expert. The mixture matching objective allows use to leverage off-policy data in imitation learning. The dual of the above mixture matching objective gives us the ReCOIL objective:

\[\max_{\pi}\min_{Q} \beta (1-\gamma)\mathbb{E}_{d_0,\pi}[Q(s,a)] +\mathbb{E}_{s,a\sim d_\text{mix}^{E,S}}[{f^*}(\mathcal{T}^{\pi}_0 Q(s,a )-Q(s,a))] -(1-\beta) \mathbb{E}_{s,a\sim d^S}[\mathcal{T}^{\pi}_0 Q(s,a )-Q(s,a)]\]

where $d_{mix}=\beta d(s,a) + (1-\beta) d^S(s,a)$ and d^E_{mix}=$\beta d^E(s,a) + (1-\beta) d^S(s,a)$.

We don’t require any restrictive assumptions on coverage, lower bounds or even a discriminator to solve the imitation learning objective. Although the above objective might appear complex, the intuition becomes clear when the function $f$ is instantiated. In the case of Chi-Square divergence, the ReCOIL objective can be simplified to:

\[\max_\pi \min_Q \beta (\mathbb{E}_{d^S,\pi(a|s)}[Q(s,a)]-\mathbb{E}_{d^E(s,a)}[Q(s,a)]) + {0.25} \color{orange} \underbrace{\color{black}\mathbb{E}_{s,a\sim d^E_{mix}}{(\gamma Q(s',\pi(s'))-Q(s,a))^2}}_{\text{Bellman consistency}}\]

The above objective learns a Q-function that ensures expert state-action pairs have higher score than other state-actions pairs. The Q-function is also learned to minimize the bellman error with 0 reward, ensuring that expert state-action pairs have higher score than other state-actions pairs.

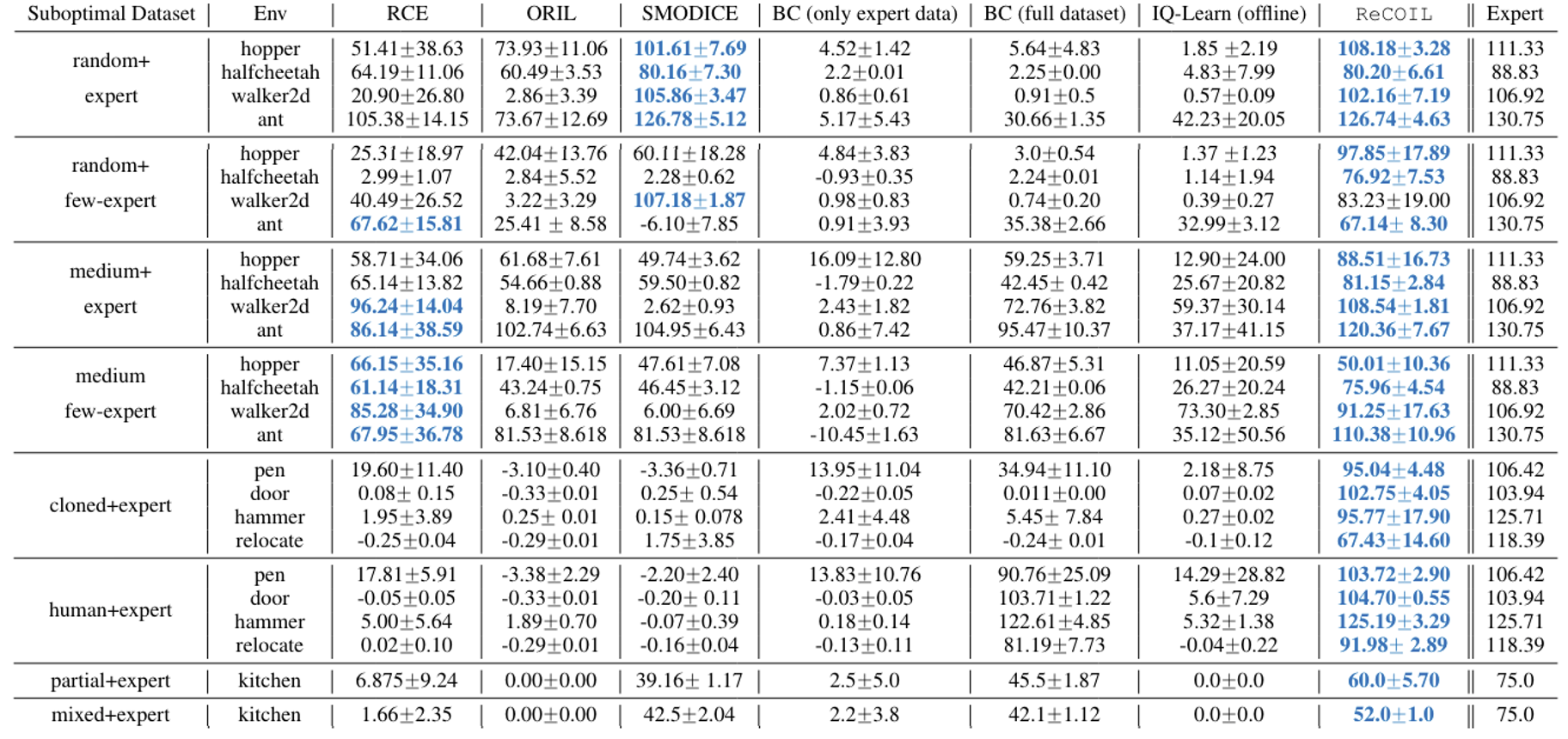
ReCOIL outperforms baselines by a wide margin as shown in figure above. This effect is particularly pronounced when the expert coverage is low or when the state is high-dimensional and methods with discriminators easily overfit. The figure below demonstrates how the previous baseline suffers from compounding errors and cannot recover in practive when trying to solve the task.

Unification

Our paper unifies many more popular algorithms (as shown in table below) in the RL literature and creates a solid foundation for understanding and developing new methods in RL. Check out our paper for more information.

Citation

If you find the work useful in your research, please consider using the following citation:

@article{sikchi2023dual, title={Dual rl: Unification and new methods for reinforcement and imitation learning}, author={Sikchi, Harshit and Zheng, Qinqing and Zhang, Amy and Niekum, Scott}, journal={arXiv preprint arXiv:2302.08560}, year={2023} }