Note: The blogs serves to promote informal understanding of the ideas in our work. For a more formal read, check out our paper.
TL;DR
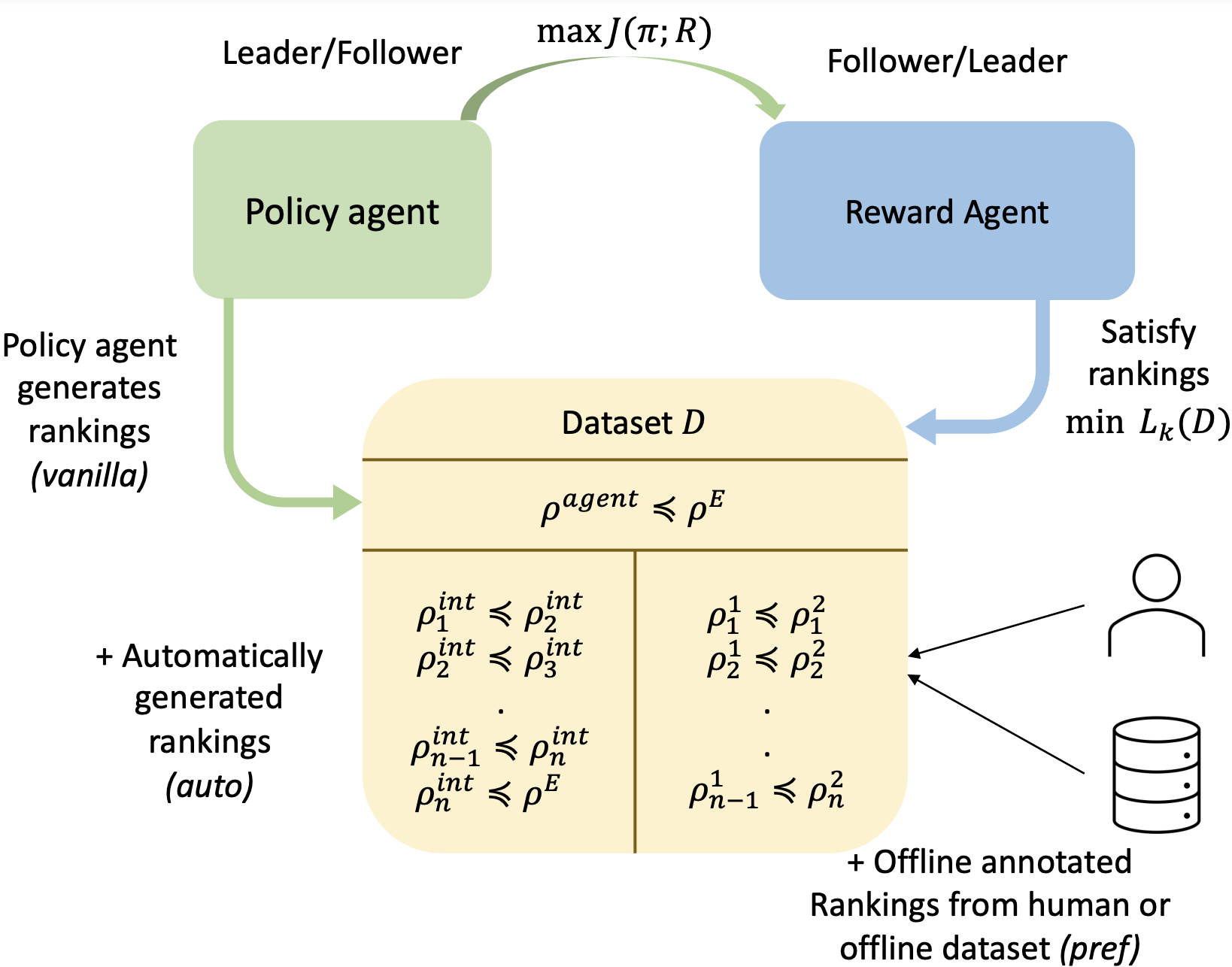
We propose $\texttt{rank-game}$ (see figure below), a new framework for imitation learning where we treat imitation as a two-player ranking-based game between a policy and a reward. In this game, the reward agent learns to satisfy pairwise performance rankings between behaviors, while the policy agent learns to maximize this reward. This framework naturally unifies learning from preferences and expert demonstrations. Our experiments show that the proposed method achieves state-of-the-art sample efficiency and can solve previously unsolvable tasks in the Learning from Observation (LfO) setting.
Why do we need a new framework?
Expert data is: ✔ Very informative of desired behavior ✘ Can be difficult to obtain ✘ Even in limit of infinite data, does not give complete information if one suboptimal behavior is better than the other
On the other hand, preferences are: ✔ Easier to obtain ✘ Required in large numbers to infer reward function
The classical inverse reinforcement learning (IRL) formulation learns from expert demonstrations but provides no mechanism to incorporate learning from offline preferences and vice versa. Our ranking game framework utilizes a novel ranking loss giving an algorithm that can simultaneously learn from expert demonstrations and preferences, gaining the advantages of both modalities.
Imitation Learning
Imitation learning (IL) involves learning from expert demonstrated behaviors. Inverse Reinforcement Learning (IRL) is a method commonly used for IL and often provides the strongest guarantees in matching expert behavior. These behaviors can be specified as sequence of observations + actions, termed as the Learning from Demonstrations (LfD) setting or they can be observations-only sequence, termed as the Learning from Observations setting (LfO). IL allows us to bypass reward specification which is in general a hard-task that often result in misaligned (with human intention) agent. While IL has been mostly limited to learning from expert demonstrations, a parallel line of work has explored using preferences between suboptimal trajectories for reward inference.
IRL objective misses a key point - incorporating suboptimal data. Why do we care about suboptimal data? Expert data is very
 informative but usually hard to obtain (eg. obtaining a running behavior from a dog, image on the right). Moreover, in the LfO setting where expert actions are missing, IRL is faced with an exploration difficulty to select actions that induce the expert observations. There are usually multiple reward hypotheses that are consistent with expert behaviors (IRL is an underspecifed problem), and this can result in reward functions that are able to imitate expert but do not capture their true intentions in parts of state-space the expert hasnt visited.
informative but usually hard to obtain (eg. obtaining a running behavior from a dog, image on the right). Moreover, in the LfO setting where expert actions are missing, IRL is faced with an exploration difficulty to select actions that induce the expert observations. There are usually multiple reward hypotheses that are consistent with expert behaviors (IRL is an underspecifed problem), and this can result in reward functions that are able to imitate expert but do not capture their true intentions in parts of state-space the expert hasnt visited.
Preferences over suboptimal data can resolve these burdens:
a. They can resolve reward ambiguity
b. They can guide policy optimization by learning a shaped reward
c. They are easy to obtain!
Our work creates a unified algorithmic framework for IRL that incorporates both expert and suboptimal information for imitation learning.
A Ranking Game for Imitation Learning
$\texttt{rank-game}$ is a simple and intuitive framework for imitation. This game is played between two players: the policy and the reward function. Reward function’s job is to take all the behavior rankings present in the dataset and learn a reward function that satisfies those rankings. The policy agent’s objective is to maximize the reward function. So what are behavior rankings and what does it mean to satisfy them? Behaviors are defined as state-action or state-only visitation distribution, i.e. places where the agent visits. A ranking between behaviors is used to specify that the expert would prefer one behavior over the other. A reward function that satisfies behavior rankings ensures that the average return under lower ranked behavior is smaller than the higher ranked behavior. More formally, the ranking game is defined as follows:
\[\underbrace{\text{argmax}_{\pi \in \Pi} J(R;\pi)}_{\text{Policy Agent}} ~~~~~ \underbrace{\text{argmin}_{R \in \mathcal{R}} L(\mathcal{D}^p;R)}_{\text{Reward Agent}}\]The policy agent $\pi$ attempts to maximize the cumulative return denoted by $J$. The reward player takes the dataset of pairwise rankings $D^p$, where the rankings are denoted as $\rho^{i} \preceq \rho^{\pi^j}$ as an input and attempts to learn a reward function that satisfies those rankings
\[\mathbb{E}_{\rho^{i}}[{R(s,a)}]\le \mathbb{E}_{\rho^j}[{R(s,a)}],~\forall \rho^{i} \preceq \rho^{j} \in \mathcal{D}^p.\]Unifying IRL and Learning-from-preferences
The $\texttt{rank-game}$ framework proposed above neatly encapsulates prior work in IRL and Learning from preferences. First, let’s see how IRL is a part of this framework. The classical IRL optimization can be written as:
\[\arg \min_{\pi\in\Pi} \sup_{f \in\mathcal{R}} \mathbb{E}_{\rho^E(s,a)}{[f(s,a)]} - \mathbb{E}_{\rho^\pi(s,a)}{[f(s,a)]}\]The inner optimization learns a reward function that ensures that the return gap under the reward function is maximized between the current policy’s behavior and the expert behavior. Thus in this case, our ranking dataset is effectively the preference that expert is better than the current agent and the ranking loss used is what we term as supremum loss (maxmizes the performance gap).
Now, when the ranking dataset only contains the offline preferences between suboptimal trajectories, and the ranking loss is set to be the Luce-Shepard loss, $\texttt{rank-game}$ reduces to previous methods like T-REX and under a bayesian setting to B-REX.
A Ranking Loss for the Reward Agent
Our proposed framework require a loss function that can ensure that the rankings are satisfied. A large class of loss function exists that accomplish this – Luce Shepard, Lovasz-Bregman Divergencs and the earlier mentioned supremum loss. While we can use any loss function that learns reward function satisfying the rankings in the dataset we would like one with nice properties. To that end, we propose a loss function called $L_k$ that attempts to induce a performance gap of $k$ between all behavior preferences in the dataset. $L_k$ is defined by the following regression loss:
\[L_k(\mathcal{D}^p;R) = \mathbb{E}_{(\rho^{\pi^i},\rho^{\pi^j})\sim \mathcal{D}^p} \Big[\mathbb{E}_{s,a\sim\rho^{\pi^i}}{[(R(s,a)-0)^2]} + \mathbb{E}_{s,a\sim\rho^{\pi^j}}{[(R(s,a)-k)^2]} \Big]\]Simply put the lower preferred behavior is regressed to a return of 0 and more preferred behavior is regressed to a return of user-defined parameter $k$. Some key properties of this loss function are:
- $L_k$ allows for learning bounded reward function with user-defined scale $k$. This is in contrast to previous Adversarial IRL approachs like GAIL, AIRL, $f$-MAX which learn unbounded rewards. A large scale of reward function makes the optimization landscape less smooth and a small scale can make the action-gap (difference of values of actions) small making the policy learning susceptible to extrapolation errors.
- The loss is principled. (a) In the setting of learning from expert demonstrations we have the vanilla rankings of the form $\text{agent}\preceq\text{expert}$. In this setting, we show that $L_k$ ranking loss minimizes the behavior divergence with the expert at convergence. (b) In the limit of infinite preferences it can recover the exact expert reward function.
- The loss by design allows for incorporation of comparison between suboptimal behaviors.
How to generate the ranking dataset?
As we have seen $L_k$ can incorporate additional preferences that can help learn a regularized/shaped reward function. This form of reward shaping can provide better guidance for policy optimization, reducing the exploration burden and increasing sample efficiency for IRL. To leverage these benefits we present two methods for augmenting the ranking dataset:
Automatically-generated rankings
It turns out we can significantly improve learning efficiency for imitation by using a dataset augmentation procedure on $D^p$. This is simply done by taking each pairwise comparison in $D^p$, say $\rho^i\preceq \rho^j$ and generating $p$ additional rankings using convex combinations of the two behaviors and assigning them increasing ranks — $\rho^i\preceq\rho^{ij}_1\preceq\rho^{ij}_2…\preceq\rho^{ij}_p\preceq\rho^j$. Here $\rho^{ij}_k = \frac{k}{p+1} \rho^i + (1-\frac{k}{p+1}) \rho^j $.
This strategy of dataset augmentation is similar to Mixup regularization commonly used in supervised learning to increase generalization and adversarial robustness. Note that here Mixup is performed in trajectory space.
Offline-annotated rankings
In situtations we have access to additional ranking — provided by humans or obtained from offline reward-annotated datasets, we can simply add them in our ranking dataset! This can significantly help in imitation by shaping the reward function, guiding policy optimization and easing exploration. We find, consistent with prior works, that LfO setting provides exploration challenges making it hard for any LfO methods to solve complex manipulation tasks. We show in our work how a handful of offline rankings can help solve such tasks.
Setting up rank-game as Stackelberg Game
We optimize the $\texttt{rank-game}$ by casting it in the Stackelberg setup. In this setup, one of the player is designated as leader and the other as follower. The idea is that since both players know the optimization objective of the other player, they can leverage this to improve stability and convergence when solving the game.
Policy as Leader (PAL): $\max_{\pi} {J(\hat{R};\pi) \,\, \text{s.t} \,\, \hat{R}=\text{argmin}_{R} L(\mathcal{D}^{\pi};R)}$
Reward as Leader (RAL): $\min_{\hat{R}}{L(\mathcal{D}^\pi;\hat{R})\,\, \text{s.t} \,\, \pi = \text{argmax}_{\pi} J(\hat{R};\pi)}$
Experiments
Asymptotic performance and sample efficiency of rank-game
We investigate the performance of $\texttt{rank-game}$ on MuJoCo locomotion tasks and benchmark it with respect to representative baselines in LfO: GAIfO, DACfO, BCO, $f$-IRL, OPOLO and IQ-Learn.

$\texttt{rank-game}$ (PAL and RAL) are the most sample efficient method outperforming the recent state-of-the-art OPOLO by a significant margin. We also require fewer line of code changes on top of SAC to achieve these results. $\texttt{rank-game}$ also achieves a higher asymptotic performance with a lower variance.
Leveraging preferences in complex manipulation tasks
Our experiments reveal that none of the prior LfO methods are able to solve complex manipulation tasks like: door opening with a parallel jaw gripper and pen manipulation with a dextrous adroit hand. This failure is potentially attributed to the exploration requirements of LfO compared to LfD coupled with the fact that in these tasks observing successes is rare which leads to poorly guided policy gradients.
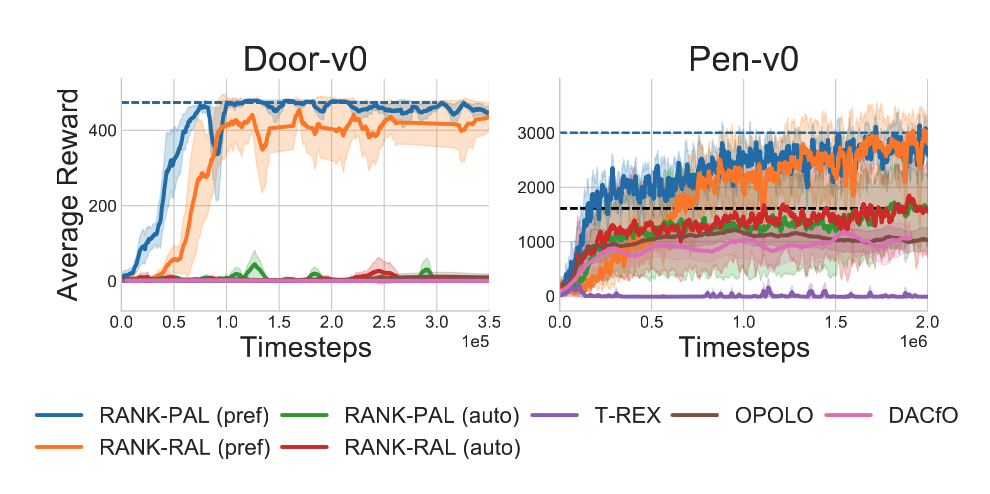
In this setting, we show that using only a handful of offline-annotated preferences in the rank-game framework can allow us to solve these tasks.
PAL vs RAL
PAL learns a reward function that is consistent with the ranking: current-agent $\preceq$ expert. RAL learns a reward function that is consistent with all the rankings that are observed during training. These properties can present certain benefits depending on the task setting.
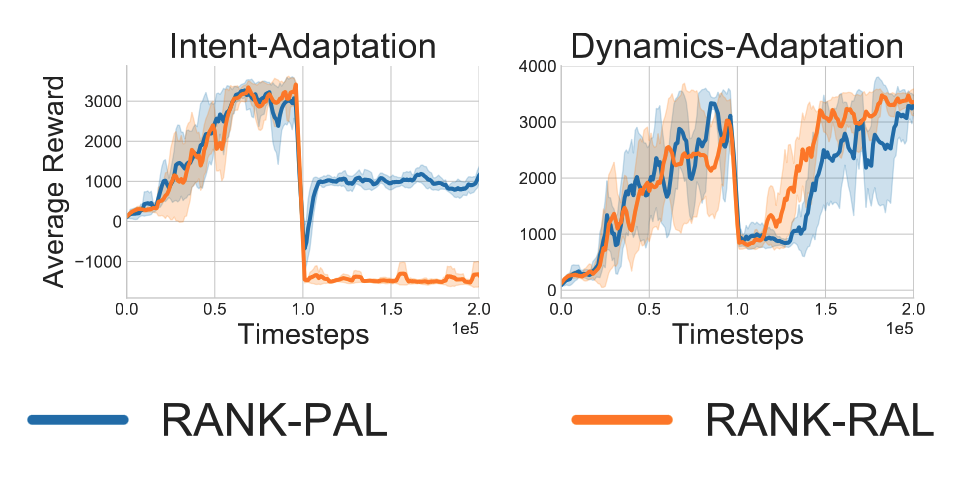
We observe that PAL adapt faster if the intent of the demonstrator changes and RAL adapts faster if the dynamics of the environment changes.
Conclusion and future work
Equipping agents to learn from different sources of information present in the world is a promising direction towards truly intelligent agents. Our framework casts imitation as a two-player ranking game unifying previous approaches of learning from expert and suboptimal behaviors.
Preferences obtained in the real world are usually noisy and one limitation of $\texttt{rank-game}$ is that it does not suggest a way to handle noisy preferences. Second, $\texttt{rank-game}$ proposes modifications to learn a reward function amenable to policy optimization but these hyperparameters are set manually. Future work can explore methods to automate learning such reward functions. Third, despite learning effective policies we observed that we do not learn reusable robust reward functions.
Citation
If you find the work useful in your research, please consider using the following citation:
@article{sikchi2022ranking, title={A Ranking Game for Imitation Learning}, author={Sikchi, Harshit and Saran, Akanksha and Goo, Wonjoon and Niekum, Scott}, journal={arXiv preprint arXiv:2202.03481}, year={2022} }